Section 1.2: Operations on Functions

Example 1

Suppose c(s) gives the number of calories burned doing s sit-ups, and s(t) gives the number of sit-ups a person can do in t minutes. Interpret c(s(3)).

When we are asked to interpret, we are being asked to explain the meaning of the expression in words. The inside expression in the composition is s(3). Since the input to the s function is time, the 3 is representing 3 minutes, and s(3) is the number of sit-ups that can be done in 3 minutes. Taking this output and using it as the input to the c(s) function will give us the calories that can be burned by the number of sit-ups that can be done in 3 minutes.

Example 2

Using the graphs below, evaluate \(f(g(1))\) .

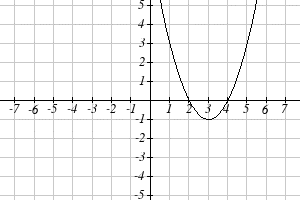
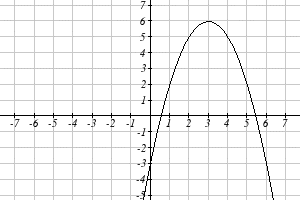
To evaluate \(f(g(1))\), we again start with the inside evaluation. We evaluate \(g(1)\) using the graph of the \(g(x)\) function, finding the input of 1 on the horizontal axis and finding the output value of the graph at that input. Here, \(g(1)=3\). Using this value as the input to the \(f\) function, \(f(g(1))=f(3)\). We can then evaluate this by looking to the graph of the \(f(x)\) function, finding the input of 3 on the horizontal axis, and reading the output value of the graph at this input. Here, \(f(3)=6\), so \(f(g(1))=6\).

Example 3

Given \(f(t)=t^2-t\) and \(h(x)=3x+2\), evaluate \(f(h(1))\).

Since the inside evaluation is \(h(1)\) we start by evaluating the \(h(x)\) function at 1: \[h(1)=3(1)+2=5\]

Then \(f(h(1))=f(5)\) , so we evaluate the \(f(t)\) function at an input of 5: \[f(h(1))=f(5)=5^2-5=20\]

Example 4

Let \(f(x)=x^2\) and \(g(x)=\dfrac{1}{x}-2x\). Find \(f(g(x))\) and \(g(f(x))\).

To find \(f(g(x))\), we start by evaluating the inside, writing out the formula for \(g(x)\):\[g(x)=\dfrac{1}{x}-2x\]

We then use the expression \(\left(\dfrac{1}{x}-2x\right)\) as the input for the function \(f\): \[f(g(x))=f\left(\dfrac{1}{x}-2x\right)\]

We then evaluate the function \(f(x)\) using the formula for \(g(x)\) as the input. Since \(f(x)=x^2\) then \[f\left(\dfrac{1}{x}-2x\right)=\left(\dfrac{1}{x}-2x\right)^2\]

This gives us the formula for the composition: \[f(g(x))=\left(\dfrac{1}{x}-2x\right)^2\]

Likewise, to find \(g(f(x))\), we evaluate the inside, writing out the formula for \(f(x)\): \(g(f(x))=g(x^2)\). Now we evaluate the function \(g(x)\) using \(x^2\) as the input: \[g(f(x))=\dfrac{1}{x^2}-2x^2\]

Example 5

A city manager determines that the tax revenue, \(R\), in millions of dollars collected on a population of \(p\) thousand people is given by the formula \(R(p)=0.03p+\sqrt{p}\), and that the city’s population, in thousands, is predicted to follow the formula \(p(t)=60+2t+0.3t^2\), where \(t\) is measured in years after 2010. Find a formula for the tax revenue as a function of the year.

Since we want tax revenue as a function of the year, we want year to be our initial input, and revenue to be our final output. To find revenue, we will first have to predict the city population, and then use that result as the input to the tax function. So we need to find \(R(p(t)).\) Evaluating this, \[\begin{align*} R(p(t)) =& R(60+2t+0.3t^2)\\ =& 0.03(60+2t+0.3t^2)+\sqrt{60+2t+0.3t^2} \end{align*}\]

This composition gives us a single formula which can be used to predict the tax revenue during a given year, without needing to find the intermediary population value. For example, to predict the tax revenue in 2017, when t = 7 (because t is measured in years after 2010), \[\begin{align*} R(p(7)) =& 0.03\left(60+2(7)+0.3\left(7^2\right)\right)+\sqrt{60+2(7)+0.3\left(7^2\right)}\\ \approx & 12.079\text{ million dollars} \end{align*}\]

Example 6

Write \(f(x)=3+\sqrt{5-x^2}\) as the composition of two functions.

We are looking for two functions, \(g\) and \(h\), so \(f(x)=g(h(x))\). To do this, we look for a function inside a function in the formula for \(f(x)\). As one possibility, we might notice that \(5-x^2\) is the inside of the square root. We could then decompose the function as: \[h(x)=5-x^2, \quad g(x)=3+\sqrt{x}\]

We can check our answer by recomposing the functions: \[g(h(x))=g(5-x^2)=3+\sqrt{5-x^2}\]

Note that this is not the only solution to the problem. Another non-trivial decomposition would be \[h(x)=x^2, \quad g(x)=3+\sqrt{5-x}.\]

Example 7

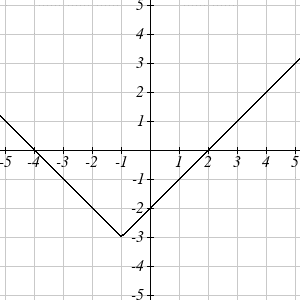
Given \(f(x)=|x|\), sketch a graph of \(h(x)=f(x+1)-3=|x+1|-3\).

The function \(\) is our toolkit absolute value function. We know that this graph has a V shape, with the point at the origin. The graph of \(h\) has transformed \(f\) in two ways: \(f(x+1)\) is a change on the inside of the function, giving a horizontal shift left by 1, then the subtraction by 3 in \(f(x+1)-3\) is a change to the outside of the function, giving a vertical shift down by 3. Transforming the graph gives:

Example 8

Write a formula for the graph shown, a transformation of the toolkit square root function.

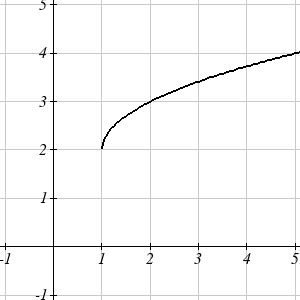
The graph of the toolkit function starts at the origin, so this graph has been shifted 1 to the right, and up 2. In function notation, we could write that as \(h(x)=f(x-1)+2\). Using the formula for the square root function we can write \(h(x)=\sqrt{x-1}+2\).

Note that this transformation has changed the domain and range of the function. This new graph has domain \([1,\infty)\) and range \([2,\infty)\).

Example 9

A common model for learning has an equation similar to \(k(t)=-2^{-t}+1\) , where \(k\) is the percentage of mastery that can be achieved after \(t\) practice sessions. This is a transformation of the function \(f(t)=2^t\) shown here. Sketch a graph of \(k(t)\).

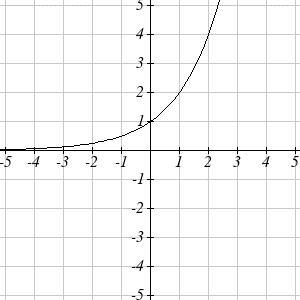
This equation combines three transformations into one equation.

A horizontal reflection:	\(f(-t)=2^{-t}\)	combined with
a vertical reflection:	\(-f(-t)=-2^{-t}\)	combined with
a vertical shift up 1:	\(-f(-t)+1=-2^{-t}+1\).

We can sketch a graph by applying these transformations one at a time to the original function:

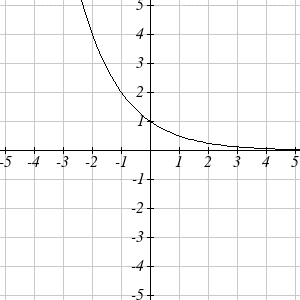
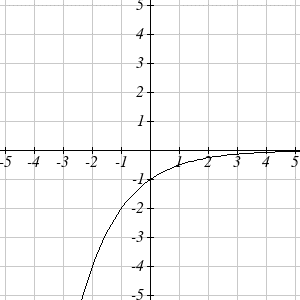
Then, after shifting up 1, we get the final graph: \[k(t)=-f(-t)+1=-2^{-t}+1\]

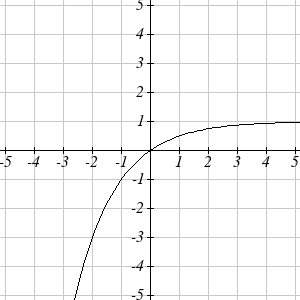
Note: As a model for learning, this function would be limited to a domain of \(t\geq 0\), with corresponding range \([0,1)\).

Example 10

The graph below is a transformation of the toolkit function \(f(x)=x^3\). Relate this new function \(g(x)\) to \(f(x)\), then find a formula for \(g(x)\).

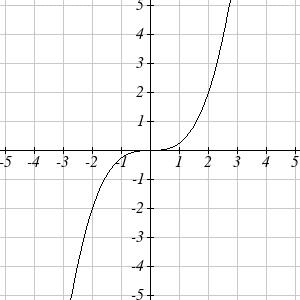
When trying to determine a vertical stretch or shift, it is helpful to look for a point on the graph that is relatively clear. In this graph, it appears that \(g(2)=2\). With the basic cubic function at the same input, \(f(2)=2^3=8\). Based on that, it appears that the outputs of \(g\) are \(\frac{1}{4}\) the outputs of the function \(f\), since \(g(2)=\frac{1}{4}f(x)\). From this we can fairly safely conclude that \[g(x)=\frac{1}{4}f(x).\]

We can write a formula for \(g\) by using the definition of the function \(f\): \[g(x)=\frac{1}{4}f(x)=\frac{1}{4}x^3.\]

Example 11

Write an equation for the transformed graph of the quadratic function shown.

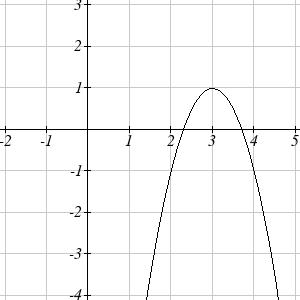
Since this is a quadratic function, first consider what the basic quadratic tool kit function looks like and how this has changed. Observing the graph, we notice several transformations: The original tool kit function has been flipped over the x axis, some kind of stretch or compression has occurred, and we can see a shift to the right 3 units and a shift up 1 unit. In total there are four operations:

1. Vertical Reflection, requiring a negative sign outside the function.
2. Vertical Stretch
3. Horizontal Shift Right 3 units, which tells us to put x-3 on the inside of the function.
4. Vertical Shift up 1 unit, telling us to add 1 on the outside of the function.

By observation, the basic tool kit function has a vertex at (0, 0) and symmetrical points at (1, 1) and (-1, 1). These points are 1 unit up and 1 unit over from the vertex. The new points on the transformed graph are 1 unit away horizontally but 2 units away vertically. They have been stretched vertically by 2.

Not everyone can see this by simply looking at the graph. If you can, great, but if not we can solve for it. First, we will write the equation for this graph, with an unknown vertical stretch:

\(f(x)=x^2\)	The original function
\(-f(x)=-x^2\)	Vertically reflected
\(-a\cdot f(x)=-a x^2\)	Vertically stretched
\(-a\cdot f(x-3)=-a(x-3)^2\)	Shifted right 3
\(-a\cdot f(x-3)+1=-a(x-3)^2+1\)	Shifted up 1

We now know our graph is going to have an equation of the form \(g(x)=-a(x-3)^2+1\). To find the vertical stretch, we can identify any point on the graph (other than the highest point), such as the point (2,-1), which tells us \(g(2)=-1\). Using our general formula, and substituting 2 for \(x\), and -1 for \(g(x)\).

This tells us that to produce the graph we need a vertical stretch by two.

Thus the function that produces this graph is \[g(x)=-2(x-3)^2+1.\]

Example 12

On what interval(s) is the function \(g(x)=\dfrac{-2}{(x-1)^2}+3\) increasing and decreasing?

This is a transformation of the toolkit reciprocal squared function, \(f(x)=\dfrac{1}{x^2}\)

\(-2f(x)=\dfrac{-2}{x^2}\)	A vertical flip and vertical stretch by 2
\(-2f(x-1)=\dfrac{-2}{(x-1)^2}\)	A shift right by 1
\(-2f(x-1)+3=\dfrac{-2}{(x-1)^2}+3\)	A shift up by 3

The basic reciprocal squared function is increasing on \((-\infty,0)\) and decreasing on \((0,\infty)\). Because of the vertical flip, the \(g(x)\) function will be decreasing on the left and increasing on the right. The horizontal shift right by 1 will also shift these intervals to the right one. From this, we can determine \(g(x)\) will be increasing on \((1,\infty)\) and decreasing on \((-\infty,1)\). We also could graph the transformation to help us determine these intervals.